د. مصطفى أبوصلاح

الاعتلاج (إنتروبي – entropy) في علم البيانات يستخدم كَمِقياس للنقاء (الخَلل) في عينة معينة. ابتكر هذا المفهوم أحد رواد المعلومات النظرية، ويدعى كلود شانون (1).

تخيل أن لدينا مجموعة تحتوي على كرات، ولكل كرة لون. ربما يكون في المجموعة أكثر من لون لهذه الكرات، تتطابق صفة أعضاء المجموعة (الكرات) إذا كانت تمتلك نفس الخواص وهنا نعني اللون. أي لو كانت جميع الكرات تمتلك نفس خاصية اللون “أحمر مثلاً” فإن المجموعة متجانسة والاعتلاج يساوي صفر. ولكن إذا اختلطت الألون بين الأخضر والأحمر بالتساوي فإن الاعتلاج سيكون 1 أي أن المجموعة في قمة عدم التجانس.

من الناحية الفنية، يمكن تعريف الإعتلاج (الإنتروبيا) على النحو التالي:

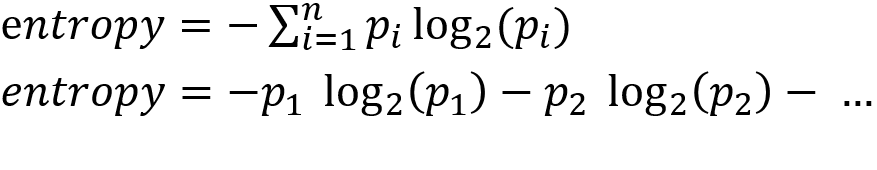
بمعنى أن الاعتلاج يساوي مجموع نسب العينات في المجموعة، حيث كل عينه تحمل نفس الخصائص تُضرب في اللوغاريتم للأساس 2 لهذه العينة والمجموع مضروب بالسالب للحصول على نتيجة موجبة. استخدام اللوغاريتم للأساس 2 هنا جاء بسبب شجرة القرارات حيث تنتهي بفرعين، مزيد من المعلومات في مرجع (1) وفي الفيديو التفصيلي في الأسفل.

أمثلة:

لنفترض أن لدينا مجموعة مكونة من عشرة كرات تحمل نفس اللون وهو الأحمر:

لو حسبنا الاعتلاج في هذه المجموعه سيكون على النحو التالي:
نسبة العينات الحمراء في المجموعة تساوي P(red)=10/10 ، وتساوي واحد الآن لنضرب الواحد في لوغاريتم الواحد
e= -(1 * log2(1))
وبما أن لوغاريتم الأساس 2 للعدد واحد يساوي صفر فإن النتيجة هي صفر أي أن العينة نقية تماماً.

الآن لنخلط العينة باللونين الأحمر والأخضر كل لون يشكل نصف المجموعة:

لنحسب الآن الاعتلاج:
e=-5/10 * log2(5/10) – 5/10 * log2(5/10)
e=-0.5*-1-0.5*-1
e=0.5+0.5
e=1
يظهر لنا أن المجموعة في قمة الإعتلاج أي عدم التجانس وذلك بسبب أن خليط اللونين متساوي.

لنأخذ هذا المثال الأخير، لدينا مجموعة فيها ثلاثة ألوان أحمر وأخضر وأصفر:

هنا سيكون الإعتلاج أعلى من معدل الإعتلاج حين كان لدينا لونين فقط. لنحسب الاعتلاج:
e=-1/10 * log2(1/10)-3/10 * log2(3/10)-6/10 * log2(6/10)
e=-0.1*-3.32-0.3*-1.74-0.6*-0.74
e=1.3
الاعتلاج يساوي تقريباً 1.3

إذن كلما قلّت الاختلافات بين خصائص الأعضاء في المجموعة قلّ الإعتلاج وكلما زادت اختلافات الخصائص ارتفع الاعتلاج.

ما هي حاجتنا لحساب الاعتلاج في علوم البيانات؟

حساب الاعتلاج في عينةٍ ما يعد متطلباً لحساب اكتساب المعلومات (Information Gain)، حيث أنه كلما زاد نقاء العينة كانت مفيدة في ارتفاع اكتساب المعلومات وكلما قل النقاء انخفض معدل اكتساب المعلومات. أحياناً نضطر لقسمة المجموعة لتحسين النقاء أي تخفيض الاعتلاج، في مثالنا الأخير لو قسمنا المجموعة إلى ثلاثة أقسام لوجدنا أن أول مجموعه وتحتوي على أربع كرات حمراء نقية الاعتلاج يساوي صفر والمجموعة الأخيرة مكونة من كرتين خضراوين أيضا الاعتلاج صفر أما المجموعة في الوسط وبها أربع كرات نجد الاعتلاج=1.5 وبهذه الحالة قمنا بتحسين العينة بعد قسمتها.

المراجع:

• (1) شانون، 1948
• (2) بروفوست، فوستر، فوسيت، توم. علوم البيانات للأعمال: ما تحتاج إلى معرفته عن استخراج البيانات والتفكير التحليلي للبيانات (مواقع Kindle 1347-1348). O’Reilly Media. اصدار حصري.