يعد الانحدار المتدرج (Gradient Descent) إلى حد بعيد استراتيجية التحسين الأكثر استخداماً في التعلم الآلي (Machine Learning) والتعلم العميق (Deep Learning) في الوقت الحالي. يتم استخدامه عند تدريب نماذج البيانات، ويمكن دمجه مع كل خوارزمية وهو سهل الفهم والتنفيذ. يجب أن يفهم كل شخص يعمل مع التعلم الآلي هذا المفهوم. سنستعرض كيفية عمل الانحدار، وأنواعه المستخدمة اليوم، ومزاياها وسلبياتها.
مقدمة في الانحدار المتدرج
الانحدار أو النزول المتدرج هو عبارة عن خوارزمية تَحسين تُستخدم عند تدريب نموذج التعلُّم الآلي. يعتمد على دالة محدبة ويقوم بتعديل مُعامِلاته (القيم الثابتة Parameters) بشكل متكرر لتقليل مَهَمَّة مُعينة إلى الحد الأدنى المحلي. بمعنى آخر:
الانحدار المتدرج هو خوارزمية تحسين للعثور على حد أدنى محلي لدالة قابلة للاشتقاق. يتم استخدام الانحدار المتدرج ببساطة للعثور على قيم المُعاملات التي تقلل دالة التكلفة (cost function) إلى أقصى حد ممكن.
تبدأ بتحديد قيم المعاملات الأولية ومن هناك يستخدم النسب المتدرج حساب التفاضل والتكامل لضبط القيم بشكل متكرر بحيث تقلل دالة التكلفة المحددة. لفهم هذا المفهوم بالكامل، من المهم معرفة التدرجات.
ما هو التدرج؟
“التدرج يقيس مقدار تغير ناتج دالة إذا تم تغيير المدخلات قليلاً.” – ليكس فريدمان (معهد ماساتشوستس للتكنولوجيا)
يقيس التدرج ببساطة التغيير في جميع الأوزان (المُتغيرات المُدخلة) وعلاقتها بالتَّغير في الخطأ. يمكنك أيضًا التفكير في التدرج على أنه مَيل دالة. كلما ارتفع التدرج، زاد الانحدار وأَسرع تعلُّم النموذج. لكن إذا انتهى الإنحدار أي أصبح مستوياً تصبح قيمة االانحدار صفراً، يتوقف النموذج عن التعلم. من الناحية الرياضية، التدرج هو مشتق جزئي فيما يتعلق بمدخلاته.

تخيل رجل معصوب العينين يريد الصعود إلى قمة جبل بأقل عدد من الخطوات قدر الإمكان للوصول للقمّة. قد يبدأ في تسلق الجبل بخطوات كبيرة في الاتجاه الأكثر انحدارًا، وهو ما يمكنه القيام به طالما أنه ليس قريبًا من القمة. عندما يقترب من القمة، ستصبح خطواته أصغر وأصغر لتجنب تجاوز القمّه. يُمكن وصف هذه العملية رياضيًا باستخدام التدرج.
تخيل الصورة أدناه توضح لنا الجبل من أعلى إلى أسفل وأن الأسهم الحمراء هي خطوات متسلقنا من القاع إلى القمة. فكر في التدرج في هذا السياق باعتباره متجهًا يحتوي على اتجاه الخطوة الأكثر حدة التي يمكن أن يتخذها الرجل معصوب العينين وكذلك المدة التي يجب أن تستغرقها هذه الخطوة.

نلاحظ أن التدرج يتفارت من الأسفل للأعلى فالخطوة من X0 إلى X1 أطول بكثير من الخطوة من X3 إلى X4. وذلك لأنَّ انحدار الجبل، الذي يحدد طول المتجه، يكون أقل. السبب هنا في قِصر الخطوة كلما تدرجنا للأعلى هو أن الإنحدار يصبح أقل حدة كلما ارتفعنا للأعلى. لذلك، كلَّما قل الإنحدار قلت الخطوة (انخفض التدرج) في مثالنا هذا كلما ارتفع المتسلق نحو قمة الجبل.
كيف يعمل الانحدار المتدرج Gradient Descent
بدلًا من تسلق الجبل، لنفكِّر في النزول المتدرج كأننا ننزل إلى أسفل الوادي. هذا تشبيه أفضل لأن خوارزميتنا تصغير دالة معيَّنة.
توضِّح المعادلة أدناه كيف يعمل النزول المتدرج: b هو الموقع التالي لمتسلقنا، بينما يمثل a موقعه الحالي. تشير علامة الطرح إلى جزء التصغير من النزول المتدرج. غاما في المنتصف هي مُعامل انتظار ومصطلح التدرج (Δf (a)) هو ببساطة اتجاه أقصى نزول.
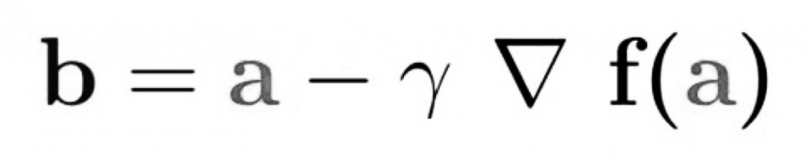
تخبرنا هذه المعادلة بشكل أساسي بالموضع التالي الذي نحتاج إلى الانتقال إليه، وهو اتجاه أقصى نزول. دعونا نلقي نظرة على مثال آخر.
تخيل أن لدينا مشكلة في التعلم الآلي ونرغب في تدريب خوارزمية عن طريق النزول المتدرج لتقليل دالة التكلفة J (w ، b) والوصول إلى الحد الأدنى المحلي عن طريق تعديل معاملاتها (w و b). توضح الصورة أدناه أن المحاور الأفقية تمثل المعاملات (w و b) ، بينما يتم تمثيل دالة التكلفة J (w ، b) على المحاور الرأسية. النزول المتدرج عباردة عن دالة محدبة.

علينا هنا إيجاد قيم w و b التي تتوافق مع الحد الأدنى من دالة التكلفة (المشار إليه بالسهم الأحمر). لبدء العثور على القيم الصحيحة، نقوم بتهيئة w و b ببعض الأرقام العشوائية. يبدأ الانحدار عند هذه النقاط (في مكان ما حول الجزء العلوي من الرسم التوضيحي)، ويستغرق خطوة تلو الأخرى في الاتجاه الانحداري الحاد (أي من أعلى الرسم التوضيحي إلى أسفله) حتى يصل إلى النقطة التي تبلغ فيها دالة التكلفة أصغر قدر ممكن.
أهمية معدل التعلم
يتم تحديد حجم الخطوات التي يأخذها النزول المتدرج في اتجاه الحد الأدنى المحلي من خلال معدل التعلم ، والذي يحدد مدى السرعة أو البطء الذي نتحرك به نحو الأوزان المثلى.
لكي يصل الانحدار إلى الحد الأدنى المحلي، يجب علينا ضبط معدل التعلم على قيمة مناسبة، وهذه القيمة يجب أن لا تكون منخفضة جدًا ولا عالية جدًا. هذا مهم لأنه إذا كانت الخطوات التي تتخذها كبيرة جدًا، فقد لا تصل إلى الحد الأدنى المحلي لأنها ترتد ذهابًا وإيابًا بين الدالة المحدبة لانحدار التدرج (انظر الصورة اليسرى أدناه). إذا قمنا بتعيين معدل التعلم على قيمة صغيرة جدًا، فسيصل انحدار التدرج في النهاية إلى الحد الأدنى المحلي ولكن قد يستغرق ذلك بعض الوقت (انظر الصورة اليمنى).

لذلك، يجب ألا يكون معدل التَّعلم مرتفعًا جدًا أو منخفضًا جدًا. يمكنك التحقق مما إذا كان معدل التَّعلم جيدًا عن طريق رسمه على الرسم البياني.
المراجع
![]()